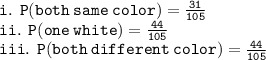Question

- Please help!! :)
Thanks in advance!​

Answer 1

`\tt i.\:\: P(both\: same\: color) =(31)/(105)\\ \tt ii.\:\: P(one\: white) = (44)/(105)\\ \tt iii. \:\:P(both\: different\: color) =(44)/(105)`

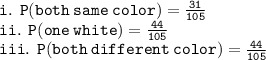
Explanation:

Note:Without Replacement:

Total no of balls=4+5+6=15 balls

i. Probability that both balls are of the same color:

First, let's calculate the probability of selecting 2 white balls:

`\tt P(2 \:white \:balls) = (4)/(15)* (3)/(14)= (12)/(210)`

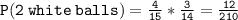
Next, let's calculate the probability of selecting 2 red balls:

`\tt P(2\: red \:balls) = (5)/(15)* (4)/(14) = (20)/(210)`

Finally, let's calculate the probability of selecting 2 black balls:

`\tt P(2 \:black\: balls) = (6)/(15)* (5)/(14)= (30)/(210)`

In order to find the probability that both balls are of the same color, we add up the probabilities for each color:

`\tt P(both \:color) = P(2\: white \:balls) + P(2 \:red \:balls) + P(2 \:black\: balls)\\ = (12)/(210) + (20)/(210) + (30)/(210)\\ = (62)/(210)\\ =(31)/(105)`

Therefore, the Probability that both balls are of the same color:
`\bold{(31)/(105)}`

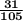
ii. Probability that one ball is white:

First, let's calculate the probability of selecting 1 white ball and 1 non-white ball:

`\tt P(1 white\: ball) = (4)/(15) * (11)/(14)= (44)/(210)`

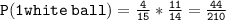
Next, let's calculate the probability of selecting 1 non-white ball and 1 white ball:

`\tt P(1\: non\: white\: ball) = (11)/(15)*(4)/(14) = (44)/(210)`

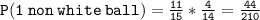
In order to find the probability that one ball is white, we add up the probabilities for each case:

`\tt P(one\: white) = P(1\: white \:ball) + P(1\: non-white\: ball)\\ =(44)/(210)+(44)/(210)\\ = (44)/(105)`

iii. Probability that both balls are of different color:

First, let's calculate the probability of selecting 1 white ball and 1 non-white ball:

`\tt P(1\: white\: ball \: and \:\:1\:non\:white\:ball) = (4)/(15) * (11)/(14)= (44)/(210)`

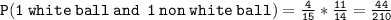
Next, let's calculate the probability of selecting 1 non-white ball and 1 white ball:

P(1 non-white and 1 white) = (11/15) * (4/14) = 44/210

`\tt P(1\: non\: white\: ball\:and\:1\:white\:ball) = (11)/(15)*(4)/(14) = (44)/(210)`

In order to find the probability that both balls are of different color, we add up the probabilities for each case:

`\tt P(both\:different\:color) = P(1\: white \:and\: 1\: non-white\: ball ) + P(1\: non-white\: and\:1\: white \:ball)\\ =(44)/(210)+(44)/(210)\\ = (44)/(105)`

Therefore, the probabilities are:

`\tt i.\:\: P(both\: same\: color) =(31)/(105)\\ \tt ii.\:\: P(one\: white) = (44)/(105)\\ \tt iii. \:\:P(both\: different\: color) =(44)/(105)`