Question

Suppose 3 persons are selected at random from a group of 7 men and 6 women. What is the probability of 2 men and 1 woman are selected?​

Answer 1

0.4406

Explanation:

Given:

Total no. of Person: 7+6=13

n= Total no. of Possible cases

n=Total no. of selection of 3 members out of 11 members.

`\tt n=C(13, 3) = (13!)/((3! * (13-3)!)) = (13*12*11*10!)/(3!*10!)=(13*12*11)/(3*2*1)=286`

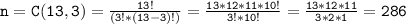
Now, let's calculate the number of ways to select 2 men and 1 woman.

We can choose 2 men from 7 men and 1 woman from 6 women:

m = No. of favorable Cases.

`\tt m=C(7, 2) * C(6, 1) = (7! )/( (2! * (7-2)!)* (6! )/(1! * (6-1)!) =(7*6*5!)/(2*1*5!) *(6*5!)/(1*5!)=21 * 6= 126`

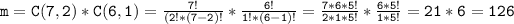
Therefore, the number of ways to select 2 men and 1 woman is 126.

The probability of selecting 2 men and 1 woman is then:

`\tt \bold{P(2\:\: men \:\: and\:\: 1\: Woman)=( No. \:of \:favorable \:Cases)/(Total\: no.\: of \:Possible\: cases\:)}`

`\tt P(2\:\: men \:\: and\:\: 1\: Woman)=(m)/(n)=(126)/(286)=0.44`

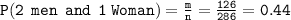
Therefore, the probability of selecting 2 men and 1 woman from the group is approximately 0.4406.