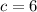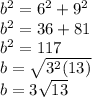Question

Look at the triangles shown below. What is the value of b ?

Answer 1

`b=3√(13)`

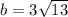
Explanation:

In a right angled triangle, if a perpendicular is drawn from a vertex of the right angle then triangles on both sides of the perpendicular are similar.

In ΔPDY, ∠D = 90° and DM ⊥ PY

So, ΔPMD ≈ ΔDMY

If two triangles are similar then their corresponding sides are proportional.

`(PM)/(DM)=(MD)/(MY)`

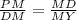
Put
`PM=4\,,\,DM=c\,,\,MD=c\,,\,MY=9`

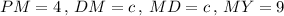
So,

`(4)/(c)=(c)/(9)\\\\c=36\\c=6`

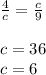
According to Pythagoras theorem, square of hypotenuse is equal to sum of squares of the other two sides.

In ΔDMY,

`DY^2=DM^2+MY^2\\b^2=c^2+9^2`

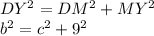
Put
`c=6`

`b^2=6^2+9^2\\b^2=36+81\\b^2=117\\b=√(3^2(13))\\b=3√(13)`