Question

Nigerian coffee costs $4.25 per 8 ounces at The Daily Grind while Bolivian coffee costs $4.50 per 8 ounces. A 50-pound mixture of these two coffees will cost $8.75 per pound. How many pounds of each kind of coffee is needed for the coffee.

​

Answer 1

Let
`x` be the number of pounds of Nigerian coffee and
`y` be the number of pounds of Bolivian coffee.

We can set up a system of equations to represent the given information:

• The cost of x pounds of Nigerian coffee is
  `\$4.25/8\: \text{oz} * 16\: \text{oz/lb} * x\: \text{lb} = \$17x`.
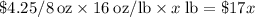• The cost of y pounds of Bolivian coffee is
  `\$4.50/8\: \text{oz} * 16\: \text{oz/lb} * y\: \text{lb} = \$18y`.
• The cost of the 50-pound mixture is
  `\$8.75/\text{lb} * 50\: \text{lb} = \$437.50`.
• The total weight of the mixture is
  `x + y = 50\:\text{ lb}`.

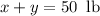So we have the following system of equations:

`\qquad\quad\begin{aligned} 17x + 18y &= 437.50 \\ x + y &= 50 \end{aligned}`

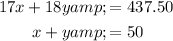
Solving this system of equations, we get:

`\qquad\qquad\quad\begin{aligned} x &= 12.5 \\ y &= 37.5 \end{aligned}`

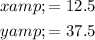
`\therefore` We need 12.5 pounds of Nigerian coffee and 37.5 pounds of Bolivian coffee for the mixture.

`\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}`

(ノ^_^)ノ
`\large\qquad\qquad\qquad\rm 06/21/2023`