Question

HURRY PLEASEE

Q.14
Using the Factor Theorem, which polynomial function has the zeros 3 and 4 – 5i?

A. x3 – 11x2 + 65x – 123
B. x2 – 7x – 5ix – 15i + 12
C. x3 – 5x2 – 15x + 27
D. x2 – x – 5ix – 15i – 12

Answer 1

The polynomial function with zeros 3 and 4 - 5i is (x-3)(x-4+5i), which simplifies to
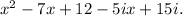`x^2 - 7x + 12 - 5ix + 15i.`Step-by-step explanation:

To find a polynomial function given its zeros, we can use the factor theorem. The factor theorem states that if a polynomial function f(x) has a zero x=a, then (x-a) is a factor of f(x).

So, the polynomial function with zeros 3 and 4 - 5i is (x-3)(x-(4-5i)). We can simplify this to (x-3)(x-4+5i).

Multiplying these factors, we get
`x^2 - 7x + 12 - 5ix + 15i.`

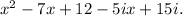
Therefore, the correct answer is B.
`x^2 - 7x - 5ix + 12 + 15i.`

Answer 2

answer : A. x3 – 11x2 + 65x – 123

if you're in a rush out the number where x is & if to get a 0 then thats probably the answer

use 3 its easier

A. 27-99+195-123= 0

C.

x3 – 5x2 – 15x + 27

27-45-45+27=-36