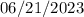Question

A full-length mirror cost $144.99 when the CPI was 163. What will a full-length mirror cost when the CPI is 211, to the nearest cent? a. $305.93 b. $214.59 c. $187.68 d. $88.95 Please select the best answer from the choices provided A B C D

Answer 1

c. $187.68

Explanation:

We Know

$144.99 when the CPI was 163

What will a full-length mirror cost when the CPI is 211?

We Take

(144.99 ÷ 163) x 211 = $187.68

So, the cost when the CPI is 211 is $187.68

Answer 2

We can use the formula for calculating inflation rate to solve for the cost of the full-length mirror when the CPI is 211:

`\text{Inflation rate}=\frac{\text{CPI in current year}-\text{CPI in base year}}{\text{CPI in base year}}* 100\%`

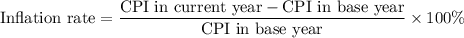
Let x be the cost of the full-length mirror when the CPI is 211. Then, we can set up the proportion:

`(211)/(163)=(x)/(144.99)`

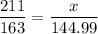
To solve for x, we can cross-multiply and simplify the equation:

`\begin{align}211* 144.99 &= 163* x \\30642.89 &= 163x \\x &= (30642.89)/(163) \\x &\approx \fbox{187.68} \\\end{align}`

`\therefore` The full-length mirror will cost approximately $187.68 when the CPI is 211, to the nearest cent.

`\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}`

(ノ^_^)ノ
`\large\qquad\qquad\qquad\rm 06/21/2023`