Question

Please help me with this! :D​

Answer 1

(i) P(B) = 0.12

(ii) P(B) = 0.2

Explanation:

A bar over a set means that we should take the complement of that set. It can also be notated by an apostrophe:

`\sf P(\overline{A \cup B})=(A \cup B)'`

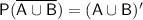
A complement of a set refers to the elements that are not included in the set, but are part of the universal set.

The symbol "∪" means the union of sets. It represents the set that contains all the elements that are in either set or in both sets.

P(A ∪ B) represents the probability of the union of sets A and B, which is the event that either A or B or both occur. Therefore, P(A ∪ B)' represents the probability of the complement of P(A ∪ B), so the probability of the event that neither A nor B occurs. Mathematically, it can be defined as:

`\boxed{\sf P(A\cup B)' = 1 - P(A\cup B)}`

`\hrulefill`

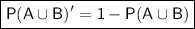
Part (i)

Mutually exclusive events are those that have no common outcomes and therefore cannot occur simultaneously. When represented using a Venn diagram, mutually exclusive events are depicted as non-overlapping circles.

The addition law for mutually exclusive events is:

`\boxed{\sf P(A \cup B)=P(A)+P(B)}`

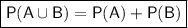
Therefore, as P(A ∪ B)' = 1 - P(A ∪ B), we can say that:

`\begin{aligned} \sf P(A \cup B)'&=\sf 1-P(A \cup B)\\ &=\sf 1-[P(A)+P(B)]\end{aligned}`

Given P(A ∪ B)' = 0.48 and P(A) =0.4, substitute these into 1 - [P(A) + P(B)] and solve for P(B):

`\begin{aligned}\sf 1-[0.4+P(B)]&=\sf0.48\\\sf1-0.4-P(B)&=\sf0.48\\\sf 1-0.4-0.48&=\sf P(B)\\\sf P(B)&=\sf0.12\end{aligned}`

Therefore, P(B) = 0.12 if events A and B are mutually exclusive.

`\hrulefill`

Part (ii)

If the probability of an event B happening doesn’t depend on whether an event A has happened or not, events A and B are independent.

The addition law for independent events is:

`\boxed{\sf P(A \cup B)=P(A)+P(B)-P(A \cap B)}`

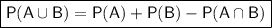
The product law for independent events is

`\boxed{\sf P(A \cap B)=P(A)P(B)}`

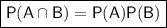
Therefore, as P(A ∪ B)' = 1 - P(A ∪ B), we can say that:

`\begin{aligned} \sf P(A \cup B)'&=\sf 1-P(A \cup B)\\ &=\sf 1-[P(A)+P(B)-P(A \cap B)]\\&=\sf 1-[P(A)+P(B)-P(A)P(B)]\end{aligned}`

Given P(A ∪ B)' = 0.48 and P(A) =0.4, substitute these into the found expression, and solve for P(B):

`\begin{aligned}\sf 1-[0.4+P(B)-0.4P(B)]&=\sf0.48\\\sf 1-[0.4+0.6P(B)]&=\sf 0.48\\\sf 1-0.4-0.6P(B)&=\sf 0.48\\\sf 0.6-0.6P(B)&=\sf 0.48\\\sf 0.6P(B)&=\sf 0.12\\\sf P(B)&=\sf 0.2\end{aligned}`

Therefore, P(B) = 0.2 if events A and B are independent.

Answer 2

i. P(B) =0.12

ii. P(B) = 0.2

Explanation:

Note:
Mutually exclusive events:

A and B are mutually exclusive events if they cannot occur at the same time. This means that A and B do not share any outcomes and

P(A AND B) = 0.

P(A ∩ B) =0

Independent events:

Two events A and B are independent events if the knowledge that one occurred does not affect the chance the other occurs.
Two events are independent if the following are true:

• P(A/B) = P(A)
• P(B/A) = P(B)
• P(A AND B) = P(A).P(B)

For Question:

i) A and B are mutually exclusive events

P((A ∪ B)')=0.48

P(A) = 0.4

Since it is mutually exclusive events

P(A ∩ B) =0

P(B)=?

We have,

P((A ∪ B)') = 1 - P(A ∪ B)

P(A ∪ B) = P(A) + P(B) - P(A ∩ B) = 0.4 + P(B) - 0 = P(B) + 0.4

Substituting value

P((A ∪ B)') = 1 - P(A ∪ B)

0.48 = 1 - P(B) - 0.4

1-P(B) - 0.4 = 0.48

Simplifying:

P(B)=1-0.4-0.48

P(B) =0.12

`\hrulefill`

ii) A and B are independent events.

P((A ∪ B)')=0.48

P(A) = 0.4

Since A and B are independent events.

P(A ∩ B) =P(A).P(B)

P(B)=?

we have,

P((A ∪ B)') = 1 - P(A ∪ B)

P(A ∪ B) = P(A) + P(B) - P(A ∩ B)= 0.4 + P(B) - 0.4 *P(B)

Substitute the values:

P((A ∪ B)') = 1 - P(A ∪ B)

0.48=1-(0.4 + P(B) - 0.4*P(B))

0.48=1-0.4-P(B)+0.4*P(B)

Simplifying:

P(B)-0.4*P(B)=1-0.4-0.48

0.6*P(B)=0.12

Dividing both sides by 0.6:

P(B) = 0.12/0.6

P(B) = 0.2