Question

....................................................................

Answer 1

13 people own a bike and a surfboard.

Explanation:

We are given a Venn diagram of members in a club who own bikes and surfboards. We are asked to find the number of people who own a bike and a surfboard.

We are given the following expressions, modeling the different categories:

• 22-y represents the number of people who only own a bike
• 14-y represents the number of people who only own a surfboard.
• y represents the number of people who own both a bike and a surfboard.
• 2 people don't own either a bike or a skateboard.
• There are 25 total members in the club.

With the above expression we can form an equation where are unknown variable is "y."

`\Longrightarrow(22-y)+y+(14-y)+2=25`

`\hrulefill`

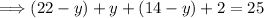
We can now use the method SCAM to help us solve this multistep equation.

`\mathbb{S}\text{implify each side of the equation using order of operations and the distributive property}\\\\ \mathbb{C}\text{ombine like terms and collect the varibles on one side}\\\\ \mathbb{A}\text{dd and/or subtract}\\\\ \mathbb{M}\text{ultiply and/or divide}`

Our goal when solving equations is to isolate the variable. Remember that anything you do to one side of the equation you must do to the other.
`\hrulefill`

Now solving:

Applying order of operations, "PEMDAS."

`\Longrightarrow(22-y)+y+(14-y)+2=25\\\\\\\Longrightarrow(1)(22-y)+y+(1)(14-y)+2=25\\\\\\\Longrightarrow22-y+y+14-y+2=25\\\\\\\Longrightarrow(-y+y-y)+(22+14+2)=25\\\\\\\Longrightarrow-y+38=25`

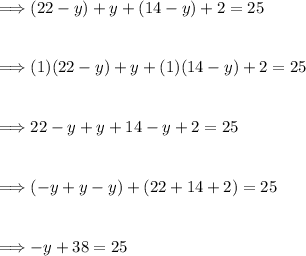
Add y to each side of the equation.

`\Longrightarrow 38=25+y`

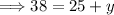
Subtract the value of 25 from each side of the equation.

`\Longrightarrow 13=y\\\\\\\therefore \boxed{\boxed{y=13}}`

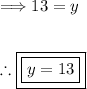
Thus, the value of y is found. Recall that the number of people who own a bike and a surfboard is equal to y. Therefore the problem is solved.