Question

The 1.2 kg rock lands on the spring and compresses it by some amount. If the spring constant is 275 N/m, how far does the rock compress the spring?

Answer 1

Approximately
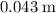`0.043\; {\rm m}` at equilibrium (assuming that
`g = 9.81\; {\rm N\cdot kg^(-1)}`.)

Step-by-step explanation:

There are two forces on this rock: the force from the spring, and weight.

Multiply the mass of the rock by
`g` to find the weight of the rock:

`\begin{aligned} (\text{weight}) &= m\, g \\ &= (1.2\; {\rm kg})\, (9.81\; {\rm N\cdot kg^(-1)}) \\ &\approx 11.772\; {\rm N} \end{aligned}`.

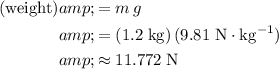At equilibrium, magnitude of the force on the rock from the spring would be equal in to that of the weight of the spring: approximately
`11.772\; {\rm N}`.

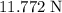To find the magnitude of the displacement of the spring, divide the magnitude of the force that the spring exerted by the spring constant:

`\begin{aligned}& (\text{displacement}) \\ =\; & \frac{(\text{spring force})}{(\text{spring constant})} \\ =\; & \frac{11.772\; {\rm N}}{275\; {\rm N\cdot m^(-1)}} \\ \approx\; & 0.043\; {\rm m}\end{aligned}`.