Question

How do i do this I’ve been struggling for 45 minutes and i can’t seem to solve it…

Answer 1

(a) start value = $45,000

(b) 4.6875 months exactly

======================================================

Step-by-step explanation

Part (a)

I'll use x in place of t, and y in place of 'a'. The reason for this will be mentioned in part (b)

• x = t = number of months
• y = a = account value in thousands of dollars

The equation
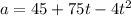`a = 45+75t-4t^2` turns into
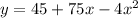`y = 45 + 75x - 4x^2` which rearranges to
`y = -4x^2+75x+45`

Let's plug in x = 0 so we can find the account value (variable y) at the very start.

`y = -4x^2+75x+45\\\\y = -4*0^2+75*0+45\\\\y = 45\\\\`

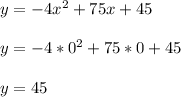
The nice thing is any term involving x will go to zero, which leaves behind 45 at the end.

The initial value is $45,000. Recall that y is the value in thousands of dollars.

Think of it like saying 45*1000 = 45,000.

-------------------

Part (b)

The template for a general quadratic is
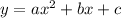`y = ax^2+bx+c` which involves 'a', so that's why I swapped to x,y to avoid confusion.

That template is used to help complete the square to get a quadratic into vertex form.

Compare
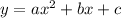`y = ax^2+bx+c` with
`y = -4x^2+75x+45` to find these values

• a = -4
• b = 75
• c = 45

Plug the first two items into the formula below

h = -b/(2a)

h = -75/(2*(-8))

h = 4.6875

This is the x coordinate of the vertex (h,k). It's the number of months it takes to reach the peak value.

-------------------

Extra info: If you plug x = 4.6875 back into the function, then you'll get y = 308.671875 which represents an account value of $308,671.88 (after rounding to the nearest penny). This is the investment's maximum value.