Question

XXX company has forecast a rate of return of 20% if the economy booms (30% probability); a rate of return of 19% if the economy in in a growth phase (40% probability); a rate of return of 2.50% if the economy in in decline (20% probability); and a rate of return of -10% if the economy in a depression (10% probability). What is the company standard deviation of returns?

Answer 1

the standard deviation of returns for XXX company is approximately 1.020 (or 102.0%). To calculate the standard deviation of returns for XXX company,

we can use the following formula: σ = √[Σ((Ri - Ravg)^2) × Pi]

Where:

σ = Standard deviation of returns

Ri = Individual return

Ravg = Average return

Pi = Probability of each return

Let's calculate the standard deviation step by step:

1. Calculate the average return (Ravg):

Ravg = (20% × 30%) + (19% × 40%) + (2.50% × 20%) + (-10% × 10%)

= 6% + 7.6% + 0.5% - 1%

= 13.1%

2. Calculate the squared differences between each return and the average return
`(Ri - Ravg)^2`:

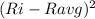For the booming economy:= (6.9%)^2 = 0.4761

For the growth phase: (19% - 13.1%)^2 = (5.9%)^2 = 0.3481

For the decline: (2.50% - 13.1%)^2 = (-10.6%)^2 = 1.1236

For the depression: (-10% - 13.1%)^2 = (-23.1%)^2 = 5.3361

3. Multiply each squared difference by its corresponding probability:

For the booming economy: 0.4761 × 0.30 = 0.1428

For the growth phase: 0.3481 × 0.40 = 0.1392

For the decline: 1.1236 × 0.20 = 0.2247

For the depression: 5.3361 × 0.10 = 0.5336

4. Calculate the sum of the weighted squared differences:

Σ((Ri - Ravg)^2) × Pi = 0.1428 + 0.1392 + 0.2247 + 0.5336 = 1.0403

5. Take the square root of the sum of the weighted squared differences to find the standard deviation:

σ = √1.0403 ≈ 1.020

Therefore, the standard deviation of returns for XXX company is approximately 1.020 (or 102.0%).