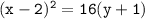Question

Find the equation for the

following parabola.
- Vertex (2,-1)
- Focus (2, 3)

A. (x-2)² = (y + 1)
B. (x-2)² = 16 (y + 1)²
C. (x-2)² = 4(y + 1)
D. (x-2)² = 16 (y + 1)

Answer 1

`\tt{D. (x-2)² = 16 (y + 1)}`

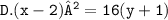
Explanation:

In order to find the equation of a parabola given its vertex and focus, we can use the standard form equation for a parabola:

`\boxed{\bold{\tt{(x - h)^2 = 4p(y - k)}}}`

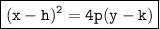
where (h, k) represents the vertex and p is the distance between the vertex and the focus.

In this case, the vertex is (2, -1) and the focus is (2, 3).

The x-coordinate of the vertex and focus are the same, which tells us that the parabola opens vertically. Therefore, the equation will have the form:

`\tt{(x - 2)^2 = 4p(y - (-1))}`

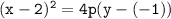
Simplifying further:

`\tt{(x - 2)^2 = 4p(y + 1)}`

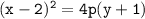
Now we need to find the value of p, which is the distance between the vertex and the focus.

The distance formula between two points (x₁, y₁) and (x₂, y₂) is given by:

`\boxed{\bold{\tt{Distance = √((x_2 - x_1)^2 + (y_2 - y_1)^2)}}}`

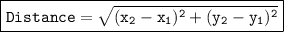
Using this formula, we can calculate the distance between the vertex (2, -1) and the focus (2, 3):

`\boxed{\bold{\tt{Distance = √((2- 2)^2 + (3 -(+1))^2)}}}`

`\boxed{\bold{\tt{Distance = √(4^2)}}}`

Distance 4

Therefore, p = 4. Substituting this value back into the equation, we get:

`\tt{(x - 2)^2 = 4(4)(y + 1)}`

`\tt{(x - 2)^2 = 16(y + 1)}`

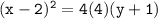
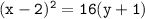
So, the equation of the parabola is
`\tt{ (x - 2)^2 = 16(y + 1)}`