The behavior of springs is governed by Hooke's Law, which states that the force required to stretch or compress a spring by some distance is proportional to that distance. Mathematically, this is expressed as:
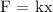
where:
-
 is the force applied,
is the force applied,
-
 is the spring constant, and
is the spring constant, and
-
 is the displacement from the spring's original position.
is the displacement from the spring's original position.
Given that a 50N force stretches the spring from 20cm to 25cm (a 5cm or 0.05m stretch), we can first calculate the spring constant
 . Then, we can use this spring constant to find the displacement when a 100N force is applied.
. Then, we can use this spring constant to find the displacement when a 100N force is applied.
Let's calculate the spring constant
 first.
first.
It seems there was a misunderstanding in the interpretation of the equation. The goal is to solve for
 , the spring constant, not
, the spring constant, not
 , the force. Let's correct this and solve for
, the force. Let's correct this and solve for
 in the equation
in the equation
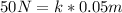 .
.
The spring constant
 is found to be
is found to be
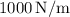 .
.
Now, let's use this spring constant to find the displacement when a 100N force is applied. We rearrange Hooke's Law to solve for
 :
:
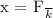
Substituting
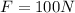 and
and
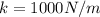 , we can find the displacement
, we can find the displacement
 .
.
The displacement
 when a 100N force is applied is 0.1 meters or 10 cm.
when a 100N force is applied is 0.1 meters or 10 cm.
Remember, this displacement is the amount the spring stretches from its original length due to the applied force. So, to find the total length of the spring when a 100N force is applied, we add this displacement to the original length of the spring (20 cm).
Let's calculate the total length of the spring.
The total length of the spring when a 100N force is applied will be 30 cm, assuming that the elastic limit is not reached.