Question

In a football game, the Beasts have three times as many points as the Beauties. The Beauties score a touchdown, worth 6 points. The Beasts now have twice as many points as the Beauties.

How many points do the Beasts have?

Answer 1

Let's denote the initial number of points the Beauties have as
`\( B \)`, and the initial number of points the Beasts have as
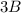`\( 3B \)` (since the Beasts have three times as many points as the Beauties).

After the Beauties score a touchdown, they have
`\( B + 6 \)` points. At this point, the Beasts have twice as many points as the Beauties, so we can write the equation
`\( 3B = 2(B + 6) \)`.

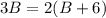We can solve this equation to find the initial number of points the Beauties had, and then use that to find the number of points the Beasts have. Let's do that.

The solution to the equation is
`\( B = 12 \)`. This means that the Beauties initially had 12 points.

Since the Beasts had three times as many points as the Beauties initially, the Beasts had
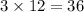`\( 3 * 12 = 36 \)` points initially.

After the Beauties scored a touchdown, they had
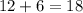`\( 12 + 6 = 18 \)` points. At this point, the Beasts had twice as many points as the Beauties, which means the Beasts still had 36 points.

Answer 2

Let's start by using algebra to solve the problem.

Let x be the number of points the Beauties have.

According to the problem, the Beasts have three times as many points as the Beauties, so the number of points the Beasts have is 3x.

When the Beauties score a touchdown, they get 6 points, so their total number of points becomes x + 6.

According to the problem, the Beasts now have twice as many points as the Beauties, so:

3x = 2(x + 6)

Simplifying this equation:

3x = 2x + 12

x = 12

Therefore, the Beauties have 12 points, and the Beasts have three times as many points, or 3x12 = 36 points.