Answer:
Approximately
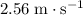 (assuming that height is measured in meters.)
(assuming that height is measured in meters.)
Step-by-step explanation:
The velocity of an object is the rate of change in the position. To find the average velocity, divide the change in position (displacement) by the length of the time interval.
In this question:
- At
 , position of the rock was
, position of the rock was
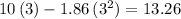 (meters.)
(meters.) - At
 , position of the rock was
, position of the rock was
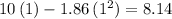 (meters.)
(meters.)
In other words, position of the rock has changed from
 to
to
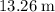 . The position of the rock has changed by
. The position of the rock has changed by
 .
.
Divide this change in position by the duration of the time interval
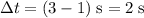 to find the average velocity of the rock:
to find the average velocity of the rock:
 .
.