Find the volume of a cone that has a radius of 2 yards and a height of 3 yards. Volume = yd³ (Use 3.14 for pi and round your answer to the nearest hundredth.)

Question

asked Apr 15, 2024 8.5k views

2 Answers

Mario Rawady · Answer 1 · 2024-04-17T03:13:06+0000

Answer:

volume of a cone = 12.56 yards³

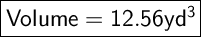
Step-by-step explanation:

volume of a cone = πr²h/3

by substituting the values,

volume of a cone = 3.14 * 2² * 3/3

= 3.14 * 4 = 12.56 yards³

Michael Speer · Answer 2 · 2024-04-19T15:32:08+0000

$\Large{\boxed{\sf Volume = 12.56yd^3}}$

$\\$

We will find the volume of the cone using the following formula:

$\Large{\sf V_(cone) = (B * h)/(3) }$

Where:

$\\$

The base of the cone is a circle, so its area can be calculated as follows:

$\Large{\sf B = \pi * r^2}$

Where:

$\\$

Replacing B with its expression in the first formula, we get:

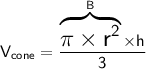
$\Large{\sf V_(cone) = \frac{\overbrace{\sf \pi * r^2}^(B) * h}{3} }$

$\\$

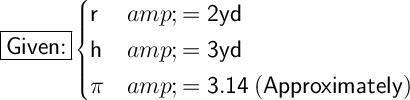
$\Large{\boxed{\sf Given \text{:} } \begin{cases} \sf r &=\sf 2yd \\ \sf h &=\sf 3yd \\ \sf \pi &= \sf 3.14 \: (Approximately) \end{cases} }$

$\\$

Substituting these values into our formula, we get:

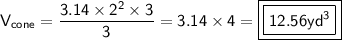
$\sf V_(cone) = (3.14 * 2^2 * 3)/(3) = 3.14 * 4 = \boxed{\boxed{\sf 12.56yd^3}}$

$\\$

Since our result has only two digits after the decimal point, we can consider it already rounded to the nearest hundredth.