Question

Help me please I need help with this question.​

Answer 1

12) B. 6.1 km

13) B. 20 cm

Explanation:

Question 12

The given diagram shows a village "V", which is 8 km on a bearing of 040° from a point O.

The scenario is modelled as a right triangle ONV, where m∠N = 90°, m∠O = 40°, and the hypotenuse OV is 8 km.

To calculate how far the village "V" is north of O, we need to find the length of side ON, which is the side adjacent to angle O.

To find ON, use the cosine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=(A)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Therefore:

`\cos 40^(\circ)=(ON)/(OV)`

`\cos 40^(\circ)=(ON)/(8)`

`ON=8\cos 40^(\circ)`

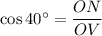
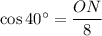
We are given cos 40° = 0.7660. Therefore, substitute this into the equation and solve for ON:

`ON = 8 \cdot 0.7660`

`ON= 6.128`

`ON= 6.1 \; \sf km\; (nearest\;tenth)`

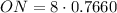
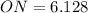
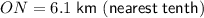
Therefore, the village "V" is 6.1 km north of O.

`\hrulefill`

Question 13

The side lengths of a rhombus are equal in length.

The diagonals of a rhombus always bisect each other at an angle of 90°.

Therefore, the two diagonals of a rhombus create 4 congruent right triangles, where each leg is half the length of each diagonal, and the hypotenuse is the side length of the rhombus.

Given the diagonals of a rhombus are 8 cm and 6 cm, the legs of each right triangle are 4 cm and 3 cm. To find the hypotenuse (side length of the rhombus), use Pythagoras Theorem:

`\begin{aligned}a^2+b^2&=c^2\\4^2+3^2&=c^2\\16+9&=c^2\\25&=c^2\\c&=5\end{aligned}`

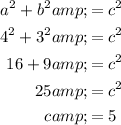
Therefore, the side length of the rhombus is 5 cm.

The perimeter of a two-dimensional shape is the distance all the way around the outside. Therefore, the perimeter of a rhombus is four times the length of one side.

`\textsf{Perimeter}=4 \cdot 5=20\;\sf cm`

Therefore, the perimeter of the rhombus is 20 cm.