Question

Please help me!!!!!!

Answer 1

3.a. 6m away

b. 3m away

Step-by-step explanation:

a)

Effort = 10000N

Load=5000 N

effort distance=3 m

load distance=?

We can use the following equation to calculate the distance of the load from the fulcrum:

`\boxed{\bold{\tt{Load * Load \:Distance = Effort * Effort \:Distance}}}`

Plugging in the known values, we get:

`\bold{\tt{5000 N * Load Distance = 10000 N * 3 m}}`

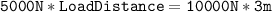
dividing both side by 5000 N

`\bold{\tt{Load\: Distance =( 10000 N * 3 m )/(5000 N)}}`

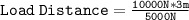
Load Distance = 6 m

Therefore, the load must be 6 meters away from the fulcrum in order for the crane to be balanced.

b)

If the load is increased to 10,000N, the effort and effort distance do not change.

Effort = 10000N

Load=10,000 N

effort distance=3 m

load distance=?

This is because the moment of the load will increase, and the moment of the effort will remain the same.

The moment of the load is calculated as follows:

`\boxed{\bold{\tt{Load * Load \:Distance = Effort * Effort \:Distance}}}`

Plugging value

`\bold{\tt{10,000 N * Load Distance = 10,000 N * 3 m}}`

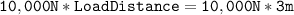
dividing both side by 10,000 N

`\bold{\tt{Load\: Distance =( 10,000 N * 3 m )/(10,000 N)}}`

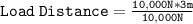
New Load Distance = 3 m

Therefore, if the load is increased to 10,000N, it should be placed 3 meters away from the pivot point to balance the crane.