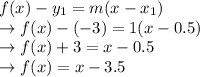Question

Find the linear function satisfying the given conditions.

A. f(−1) = 0 and f(7) = 2. f(x) = ?

B. f(1/2)= -3 and the graph of 'f' is a line parallel to the line x-y= 4. f(x) = ?

Answer 1

A. f(x) = 4x + 4

B. f(x) = x - 3.5

Explanation:

A. Let's first break down the givens.

When we're given that
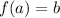`f(a) = b`, for any a and b, that means that the point (a, b) exists on the graph of f(x).

Following this logic, we're given two points on the graph of f(x): (-1, 0) and (7, 2).

Using these two points, we can first find the slope of the function:

`m = (y_2 - y_1)/(x_2 - x_1) = (7 - (-1))/(2 - 0) = \frac82 = 4`

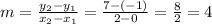
Now we can substitute one of the points, as well as the slope, to find the equation of the graph:

`f(x) - y_1 = m(x - x_1)\\\to f(x) - 0 = 4\left(x - (-1)\right)\\\to f(x) = 4x + 4`

B. Breaking down the givens, we know two things:

- The point (0.5, -3) exists on the graph f(x)

- The slope of the function is the same as the given line y. This is because parallel lines have the same slope. The equation of line y is
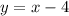`y = x -4`, meaning that the slope is 1.

Substituting the given point and the slope to find the equation of the graph:

`f(x) - y_1 = m(x - x_1)\\\to f(x) - (-3) = 1(x - 0.5)\\\to f(x) + 3 = x - 0.5\\\to f(x) = x - 3.5`