Find the exact location of all the relative and absolute extrema of the function f(x) = 2x²-4x-6 with domain [0,3]. There should be three answers.

Question

asked Feb 16, 2024 208k views

1 Answer

Rumi · Answer 1 · 2024-02-21T07:34:06+0000

Explanation:

Take the derivative of the function.

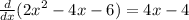
$(d)/(dx) ( {2x}^(2) - 4x - 6) = 4x - 4$

Set the derivative function equal to 0.

4x - 4 = 0

x = 1

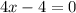
Next, we use sign analysis to see where we have relative max/min, absolute max/min

We also include the endpoints of the interval as well (0,3)

So we have two intervals

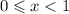
$0 \leqslant x < 1$

$1 < x \leqslant 3$

For every interval, pick a random point to see if the derivative function is positive or negative.

If positive, that interval is increasing

If negative, that interval is decreasing.

If 0, that interval is constant

For the first interval, let use 0

4(0) - 4 = - 4

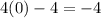
So the interval is decreasing over 0<=x<1

Furthermore, since the interval is decreasing. The intial point at x=0 could be considered a maximum.

For the second interval, let use 2

4(2) - 4 = 4

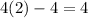
So the interval is increasing over 1<x<=3,

Furthermore, since the interval is increasing. The enpoint could also be considered a maximum.

Since we went from decreasing to increasing, the point

x = 1

can be considered a minimum point.

Let plot all the critical values in the function to see their coordinate pair.

f(0) = - 6

f(1) = - 12

f(3) = 0

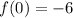
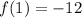
So here

(0,-6) is a relative maximum

(1,-12) is a absolute minimum

(3,0) is a absolute maximum