Question

Given: Isosceles right triangle XYZ (45°–45°–90° triangle)

Prove: In a 45°–45°–90° triangle, the hypotenuse is StartRoot 2 EndRoottimes the length of each leg.

Triangle X Y Z is shown. Angle X Y Z is 90 degrees and the other 2 angles are 45 degrees. The length of X Y is a, the length of Y Z is a, and the length of X Z is c.

Because triangle XYZ is a right triangle, the side lengths must satisfy the Pythagorean theorem, a2 + b2 = c2, which in this isosceles triangle becomes a2 + a2 = c2. By combining like terms, 2a2 = c2.

Which final step will prove that the length of the hypotenuse, c, is StartRoot 2 EndRoot times the length of each leg?

Substitute values for a and c into the original Pythagorean theorem equation.
Divide both sides of the equation by two, then determine the principal square root of both sides of the equation.
Determine the principal square root of both sides of the equation.
Divide both sides of the equation by 2.

Answer 1

C, take the square root of both sides of the equation.

Explanation:

At the end of the proof, we have
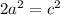`2a^(2) =c^(2)`. Since we want to prove that
`c=a√(2)`, we can take the square root on both sides of the first equation to get
`\sqrt{2a^(2) } =\sqrt{c^(2) }`.

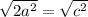Since the square root of a squared is a, and the square root of c squared is c, we have:

`a√(2) =c`.

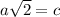Therefore, we have proved that the hypotenuse is the length of each leg times the square root of two, and therefore we need to take the square root of each side of the equation to do so.

The answer option that does this is C.