Answer: The distance between the complex numbers is approximately
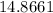 or
or

Explanation:
The distance between two complex numbers
 is given by the formula:
is given by the formula:

This formula is similar to the Euclidean distance formula in two dimensions, where
 and
and
 represent the x and y coordinates of the first point, and
represent the x and y coordinates of the first point, and
 and
and
 represent the x and y coordinates of the second point.
represent the x and y coordinates of the second point.
In this case, the two complex numbers are
 and
and
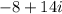 . So,
. So,
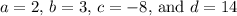 .
.
Substituting these values into the formula, we get:

So, the distance between
 and
and
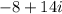 is
is
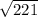 , which is approximately
, which is approximately
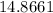 or
or
