Question

A man covers 1/3rd of his journey at 15 km/hr & the

remaining at 20 km/hr. If he takes 10 hrs to complete his Journey find the length of his journey​

Answer 1

1/3 of his journey=15km/hr &

the remaining at 20 km/hr

20/15/5 =

20/5 =4

15/5= 3 =4*3=

12+10= 22

Answer 2

180 km

Explanation:

To find the length of the journey, use the time-distance-speed formula.

Let the length of the journey = x km

We know that,

`\boxed{\bf Time = (Distance )/(Speed)}`

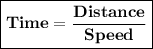
Case 1:

`\sf (1)/(3)^(rd) \ \text{of the journey} = (1)/(3)x`

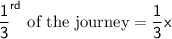
Speed = 15 Km/hr

`\sf \text{Time taken to cover one-third of the journey}=(1)/(3)x / 15`

`\sf = (1)/(3)x*(1)/(15)\\\\=(1)/(45)x`

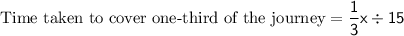
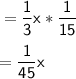
Case 2:

`\sf Remaining \ distance = (2)/(3)x`

`Speed = 20 \ km /hr`

`\sf \text{Time take to cover two-third of the distance = }(2)/(3)x / 20`

`\sf = (2)/(3)x*(1)/(20)\\\\\\=(1)/(3)x*(1)/(10)\\\\=(1)/(30)x`

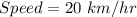
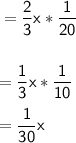
Total time taken to complete the journey = 10 hrs

`\sf~~~~~~~ (1)/(45)x+(1)/(30)x= 10\\\\\\LCM \ of \ 45 \ \& \ 30 = 90\\\\(1*2)/(45*2) x+(1*3)/(30*3)x=10\\\\\\~~~~~~~~~~(2)/(90)x+(3)/(90)x=10\\\\\\~~~~~~~~~~~~~~~~~~~ (5)/(90)x=10\\\\\\`

`\sf x = 10*(90)/(5)\\\\x = 180 \ km`

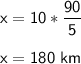
Length of the journey = 180 km