Question

Salma, All, and Jose sent a total of 129 text messages over their cell phones during the weekend. Ali sent 3 times as many messages as Jose. Jose sent 9 fewer

messages than Salma. How many messages did they each send?

Answer 1

Let the number of messages that Salma sent be ex.

This means that Jose sent x-9 messages as he had sent 9 fewer messages than Salma.

Ali sent 3 times the number of messages that Jose sent. As Jose sent x-9 messages, Ali must have sent 3(x-9) messages.

The total number of messages is 129. So,

(x+ (x-9) + 3 (x-9) = 129
x + x-9 + 3x - 27 = 129
5x = 129 + 36
x = 165 divided by 5
= 33

Therefore, Salma sent 33 messages, Jose sent 33-9 = 24 messages, and Ali sent 3x 24 = 72 messages.

Answer 2

Salma = 33 text messages

Ali = 72 text messages

Jose = 24 text messages

Explanation:

Let "s" be the number of text messages Salma sent.

Let "a" be the number of text messages Ali sent.

Let "j" be the number of text messages Jose sent.

From the given information and defined variables, create a system of equations:

`\begin{cases}s + a + j = 129\\a = 3j\\s=j+9\end{cases}`

Substitute the second and third equations into the first equation to create an equation with only the variable j:

`s+a+j=129`

`j+9+3j+j=129`

Solve for j:

`5j+9=129`

`5j+9-9=129-9`

`5j=120`

`5j / 5=120 / 5`

`j=24`

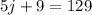
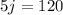
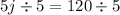
Therefore, Jose sent 24 text messages.

Substitute the found value of j into the second and third equations to find the values of a and s:

`a=3(24)=72`

`s=24+9=33`

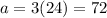
Therefore, Ali sent 72 text messages and Salma sent 33 text messages.

Therefore, in conclusion:

• Salma sent 33 text messages.
• Ali sent 72 text messages.
• Jose sent 24 text messages.