Question

The length of a rectangle is three times its width.

If the perimeter of the rectangle is 40 ft , find its area.

Answer 1

The answer is:

A = 75 ft²

Work/explanation:

The sides of the rectangle are given as:

`\sf{Length=3~times~the~width}`

`\sf{Width=unknown}`

I will go ahead and call the width x, then the length will be 3x.

So now, we plug the values into the perimeter formula:

`\sf{P=2(l+w)}`

where P = perimeter;

l = length;

w = width.

Plug in the numbers; knowing that P = 40, l = 3x, w = x:

`\sf{40=2(3x+x)}`

Solve for x

`\sf{2(3x+x)=40}`

`\sf{2(4x)=40}`

`\sf{8x=40}`

`\sf{x=5}`

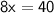
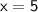
The length is thus 3x = 3(5) = 15 ft.

Now we move on to the next part of the question, where we're asked to find the rectangle's area. And now we know both the length and the width of the rectangle, we can go right ahead and plug the numbers into the formula, which is
`\boldsymbol{A=LW}`.

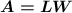Where A = area;

L = length;

w = width.

Plug in the values:

`\boldsymbol{A=15*5}\\\\\\\boldsymbol{A=75\:ft^2}`

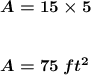
Hence, that is the area.

Answer 2

75 ft²

Explanation:

`L=3W\\2W+2L=40\\\\2W+2(3W)=40\\2W+6W=40\\8W=40\\W=5\\\\L=3(5)=15`

Since the width of the rectangle is 5 ft and the length is 15 ft, then its area would be 5*15 = 75 ft².