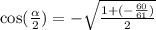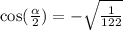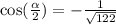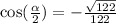Question

How would I solve this?

Answer 1

Explanation:

In these types of problems, you need to use various trigonometric identities to solve this.

First, note what are you trying to solve.

We are trying to find

`\cos( ( \alpha )/(2) )`

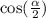
Using our trig identities, we know that

`\cos( ( \alpha )/(2) ) = \sqrt{ (1 + \cos( \alpha ) )/(2) }`

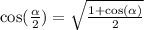
Next, in order to solve this problem, we need to find cos(alpha).

So using our given info, of tan(alpha), we must find a way to manipulate that information to get cos(alpha)

Notice that

`\tan {}^(2) ( \alpha ) + 1 = \sec {}^(2) ( \alpha )`

`\sqrt{ \tan {}^(2) ( \alpha ) + 1 } = \sec( \alpha )`

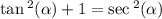
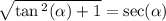
And that

`\cos( \alpha ) = (1)/( \sec( \alpha ) )`

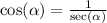
So,

`\cos( \alpha ) = \frac{1}{ \sqrt{ \tan {}^(2) ( \alpha ) + 1 } }`

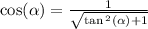
Using the interval, since cos is negative over the interval (pi,3pi/2),

our answer will be negative

`\cos( \alpha ) = - \frac{1}{ \sqrt{ \tan {}^(2) ( \alpha ) + 1 } }`

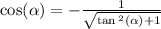
We know that

`\tan( \alpha ) = (11)/(60)`

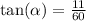
So

`\cos( \alpha ) = - \frac{1}{ \sqrt{( (11)/(60) ) {}^(2) + 1 } }`

`\cos( \alpha ) = - \frac{1}{ \sqrt{ (121)/(3600) + 1} }`

`\cos( \alpha ) = - (1)/( (61)/(60) )`

`\cos( \alpha ) = - (60)/(61)`

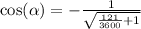
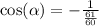
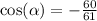
Since we know what cos(alpha) is, We can solve cos(alpha/2), likewise, cos will be negative since the former is negative over pi and 3pi/2

`\cos( ( \alpha )/(2) ) = - \sqrt{ (1 + ( - (60)/(61) ))/(2) }`

`\cos( ( \alpha )/(2) ) = - \sqrt{ ( (1)/(61) )/(2) }`

`\cos( ( \alpha )/(2) ) = - \sqrt{ (1)/(122) }`

`\cos( ( \alpha )/(2) ) = - (1)/( √(122) )`

`\cos( ( \alpha )/(2) ) = - ( √(122) )/(122)`