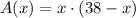Question

A daycare has 38 ft of dividers with which to enclose a rectangular play space in a corner of a large room. The sides against the wall require no partition. Suppose the play space is x feet long. Express the area A of the play space as a function of x. A(x)=

Answer 1

The daycare is using dividers to enclose a rectangular play space in a corner of a large room. This means that two sides of the rectangle are against the wall and do not require dividers. The other two sides of the rectangle, which are not against the wall, will be enclosed by the dividers.

Let's denote the length of the rectangle as x feet and the width as y feet. The total length of the dividers, which is 38 feet, is equal to the sum of the length and the width of the rectangle, or x + y. We can express y in terms of x as follows:

`\(y = 38 - x\)`

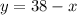
The area A of the rectangle is given by the product of the length and the width, or
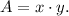`\(A = x \cdot y\).` Substituting
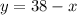`\(y = 38 - x\)` into this equation, we get the area x as a function of x:

`\(A(x) = x \cdot (38 - x)\)`