Question

Find the values of x (there are two) when the ratio of the area of the shaded portion of the figure to the total area of the figure is 15.75/48.

Hint: First, set up a ratio between the areas of the two triangles. Remember that the area of a triangle is calculated by: A=1/2bh

Answer 1

Explanation:

the hint they give you is right, if you follow that you'll get

shaded area= (x+0.5)(x+1.5)/2

shaded area= (x²+2x+0.75)/2

shaded area= ½x² + x + 0.375

total area= (2x)(x+5)/2

total area= x² + 5x

since the ratio

`(shaded \: area)/(total \: area) = (15.75)/(48) = \frac{0.5 {x}^(2) + x + 0.375}{ {x}^(2) + 5x}`

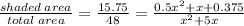
rearranging the terms you'll get

(15.75)(x²+5x)=(0.5x²+x+0.375)(48)

15.75x²+78.75x = 24x²+48x+18

-8.25x²+30.75x-18=0

using the quadratic formula you'll get the values

x1=3

x2=0.727