Question

I NEED HELP ASAP! :)

Answer 1

Answer: The maximum 38 at (1,2)

===================================================

Step-by-step explanation:

The inequality of
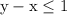`\text{y}-\text{x} \le 1` solves to
`\text{y} \le \text{x}+1`

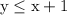
The boundary line equation is
`\text{y} = \text{x}+1`

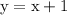
That line goes through (0,1) and (1,2). It is a solid line because of the "or equal to" portion. Points on the boundary are included in the shaded solution set.

We'll shade below the boundary because of the "less than" portion when y is isolated.

-------------

Let's do the same for the second inequality.

`9\text{x}+3\text{y} \le 15\\\\3\text{y} \le -9\text{x}+15\\\\\text{y} \le \frac{-9\text{x}+15}{3}\\\\\text{y} \le \frac{-9\text{x}}{3}+(15)/(3)\\\\\text{y} \le -3\text{x}+5\\\\`

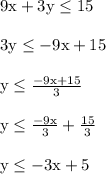
The boundary equation is y = -3x+5 which goes through (0,5) and (1,2)

We shade below this solid boundary line.

We'll shade to the right of x = -3 and above y = -4 due to the third and fourth inequalities given.

From here we overlap the four shaded regions to get what you see in the image attachment below.

I used Desmos to make the graph. GeoGebra is another good option.

-------------

The vertex or corner points are

• (-3,-2)
• (-3,-4)
• (3,-4)
• (1,2)

We need to test each of them with the objective function.

Let's try the coordinates of (-3,-2)

P = 2x+6y+24

P = 2*(-3)+6*(-2)+24

P = 6

Now try (-3,-4)

P = 2x+6y+24

P = 2*(-3)+6*(-4)+24

P = -6

Now try (3,-4)

P = 2x+6y+24

P = 2*(3)+6*(-4)+24

P = 6

Lastly we need to try (1,2)

P = 2x+6y+24

P = 2*(1)+6*(2)+24

P = 38

This produces the largest value of P.

Therefore, the max is 38 and occurs at (1,2)