Question

Factorise : x^3+13x^2+32x+20​

Answer 1

Explanation:

x³+13x²+32x+20 is

x³+x²+12x²+20x+20

=x²(x+1)+12x(x+1)+20(x+1)

=(x-1)(x²+12x+20)

=(x-1) (x²+10x+2x+20)

=(x+1)[x(x+10)+2(x+10)]

=(x+1)(x+2)(x+10)

hope it helps

Answer 2

(x + 1)(x + 2)(x + 10)

Explanation:

Start by listing the factors of 20, which are ±1, ±20, ±2, ±10, ±4, ±5. Next, substitute one of the factors and observe if the polynomial becomes 0. What we are trying to find is finding the factor of the polynomial.

Try x = -2:

`\displaystyle{\text{P}(-2)=(-2)^3+13(-2)^2+32(-2)+20}\\\\\displaystyle{\text{P}(-2)=-8+52-64+20}\\\\\displaystyle{\text{P}(-2)=0}`

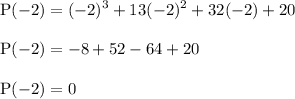
Since x = -2 makes the polynomial equal to 0. Therefore, we can say that x + 2 is a factor of the polynomial. Then we divide the polynomial by the factor x + 2:

`\displaystyle{\begin{array}{r}x^2+11x+10\phantom{)} \\x+2{\overline{\smash{\big)}\,x^3+13x^2+32x+20\phantom{)}}}\\\underline{-~\phantom{(}(x^3+2x^2)\phantom{-b)}}\\11x^2+32x\phantom{)}\\ \underline{-~\phantom{()}(11x^2+22x)}\\ 10x+20\phantom{)}\\\underline{-~\phantom{()}(10x+20)}\\ 0\phantom{)}\\\end{array}}`

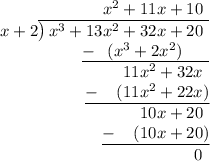
Thus:

`\displaystyle{(x^3+13x^2+32x+20)/(x+2)=x^2+11x+10}`

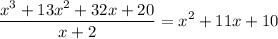
Multiply x + 2 both sides, therefore:

`\displaystyle{x^3+13x^2+32x+20=\left(x+2\right)}\left(x^2+11x+10\right)}`

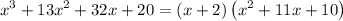
Factor the quadratic expression:

`\displaystyle{\left(x+2\right)\left(x^2+11x+10\right) = \left(x+2\right)\left(x+10\right)}\left(x+1\right)}`

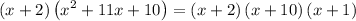
Therefore, the factored expression is (x + 2)(x + 10)(x + 1)