Question

Given that 2y-3x=5, Find the gradient and y intercept of the line?​

Answer 1

The gradient is:

3/2

The y intercept is:

5/2

Work/explanation:

Let's rearrange the equation first so that it's in slope intercept.

Our equation is

`\bf{2y-3x=5}`

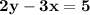
And we should write it in
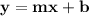`\bf{y=mx+b}` form. Let's go ahead and perform the required operations.

________________________

Add 3x on each side:

`\bf{2y=5+3x}`

`\bf{2y=3x+5}`

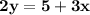
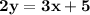
Now, divide each side by 2:

`\bf{y=(3)/(2)x+(5)/(2)}`

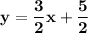
This is the equation in slope intercept.

As for the gradient, that is the number in front of x : 3/2.

As for the y intercept, that is the constant : 5/2

Hence, these are the answers.

Answer 2

gradient =
`(3)/(2)` , y- intercept =
`(5)/(2)`

Explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the gradient and c the y- intercept )

given

2y - 3x = 5 ( add 3x to both sides )

2y = 3x + 5 ( divide through by 2 )

y =
`(3)/(2)` x +
`(5)/(2)` ← in slope- intercept form

with gradient m =
`(3)/(2)` and y- intercept c =
`(5)/(2)`