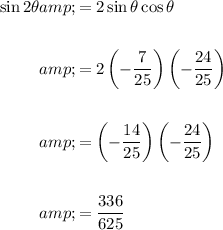Question

Given sinx equals -7/25 and pi

Answer 1

B

Explanation:

`\sin(2 \alpha ) = 2 \sin( \alpha ) \cos( \alpha )`

So we must find cos(alpha)

Use the Pythagorean Identity

`\sin {}^(2) (x) + \cos {}^(2) (x) = 1`

We know sin(x)=-7/25

`( - (7)/(25) ) {}^(2) + \cos {}^(2) ( \alpha ) = 1`

`\cos {}^(2) ( \alpha ) = 1 - (49)/(625)`

`\cos {}^(2) ( \alpha ) = (576)/(625)`

`\cos( \alpha ) = (24)/(25)`

Since cos Is negative over the 3rd quadrant,

`\cos( \alpha ) = - (24)/(25)`

So we solve sin(2theta)

`\sin(2 \alpha ) = 2( ( - 7)/(25) )( ( - 24)/(25) )`

`= (336)/(625)`

Answer 2

`\textsf{B)} \quad (336)/(625)`

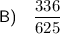
Explanation:

The sine double angle identity is:

`\boxed{\sin (A\pm B)=\sin A \cos B\pm\sin B\cos A}`

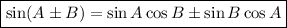
Therefore, using the sine double angle identity, we can rewrite sin 2θ as:

`\sin (\theta+\theta)=\sin \theta \cos \theta+\sin \theta \cos \theta`

`\sin 2\theta=2 \sin \theta \cos \theta`

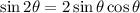
Given that sin θ = -7/25, we can use the trigonometric identity sin²θ + cos²θ = 1 to find cos θ:

`\sin^2 \theta+\cos^2 \theta=1`

`\left(-(7)/(25)\right)^2+\cos^2 \theta=1`

`\cos^2 \theta=1-\left(-(7)/(25)\right)^2`

`\cos \theta=\sqrt{1-\left(-(7)/(25)\right)^2}`

`\cos \theta=(24)/(25)`

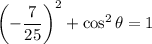
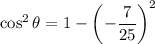
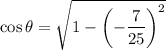
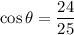
The given interval for angle θ is:

`\pi < \theta < (3\pi)/(2)`

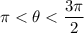
From inspection of the unit circle (attached), we can see that angle θ is in quadrant III. In this quadrant, both the sine and cosine of the angle are negative. Therefore:

`\cos \theta=-(24)/(25)`

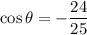
Substitute the given value of sin θ and the found value of cos θ into the double angle equation to find the exact solution of sin 2θ:

`\begin{aligned}\sin 2 \theta&=2 \sin \theta \cos \theta\\\\&=2 \left(-(7)/(25)\right) \left(-(24)/(25)\right)\\\\&= \left(-(14)/(25)\right) \left(-(24)/(25)\right)\\\\&= (336)/(625)\\\\\end{aligned}`