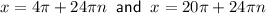Question

The model for long-term average temperature f(x), in degrees Celsius, at the Willburn airport is represented by the equation

f(x)=5cos(x/12)+14.5.
If x represents the month of the year, in which months will the temperature be 17°C?

Answer 1

`x=4\pi+24\pi n\;\;\textsf{and}\;\;x=20\pi+24\pi n`

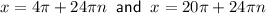
Explanation:

The function f(x) models the long-term average temperature in degrees Celsius, where x represents the month of the year:

`f(x)=5 \cos \left((x)/(12)\right)+14.5`

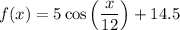
To find the months when the temperature will be 17°C, set f(x) equal to 17 and solve for x.

`5 \cos \left((x)/(12)\right)+14.5=17`

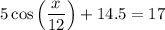
Subtract 14.5 from both sides of the equation:

`5 \cos \left((x)/(12)\right)=2.5`

Divide both sides of the equation by 5:

`\cos \left((x)/(12)\right)=0.5`

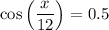
Take the inverse cosine of both sides of the equation:

`(x)/(12)=\cos^(-1)(0.5)`

`(x)/(12)=(\pi)/(3)+2\pi n,(5\pi)/(3)+2\pi n`

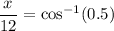
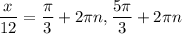
Multiply both sides by 12:

`x=4\pi+24\pi n,20\pi+24\pi n`

Therefore, the months in which the temperature will be 17°C are:

`x=4\pi+24\pi n\;\;\textsf{and}\;\;x=20\pi+24\pi n`