Answer:
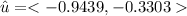
Explanation:
To find the direction in which the maximum rate of change occurs for the function f(x,y)=2xsin(xy) at the point (1, 3), we need to find the gradient vector and normalize it to obtain a unit vector.
The gradient vector of a function f(x,y) is given as:
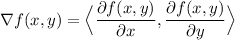
Taking the partial derivatives.
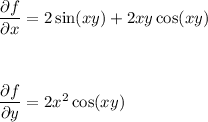
Evaluate these at the point (1,3).

Thus, we have:
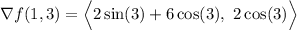
To obtain the unit vector in the direction of maximum rate of change, we need to normalize the gradient vector:

Thus, the problem is solved.