Answer:
Explanation:
Before we do anything, let convert the line to slope intercept form
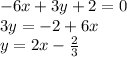
Now let understand the methodology of this problem:
The shortest distance between a point and a line is a line segment that is perpendicular to the line that also pass through the point.
So, this is what we need to do,
1. Find a line that is perpendicular to the original line and pass through the point (0,-3)
2. Find the intersection point of the two lines.
Step 1:
The slope of the new line should be -1/2 since that is the negative reciprocal of the original line slope.
The point should pass through (0,-3) , so let use point slope form.
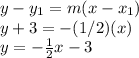
Step 2: Find the intersection point of the lines.
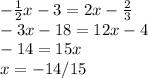
Find the y coordinate of the point by plugging in (-14/15) for the function in either.
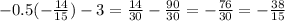
So the point on the line, that is closest to the point (0,-3),
(-14/15, -38/15)