Question

A 5. 70-kg box is sliding across the horizontal floor of an elevator. The coefficient of kinetic friction between the box and the floor is 0. 400. Determine the kinetic frictional force that acts on the box when the elevator is accelerating downward with an acceleration whose magnitude is 1. 10 m/s2

Answer 1

Approximately
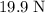`19.9\; {\rm N}`, assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.

Step-by-step explanation:

The kinetic friction between the ground and the box can be found by multiplying the normal force on the box by the coefficient of kinetic friction. While the normal force on the box isn't given, this value can be found from the net force on the box.

It is given that the elevator is accelerating downward at
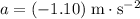`a = (-1.10)\; {\rm m\cdot s^(-2)}` (negative since the elevator is accelerating downward.) The vertical acceleration of the box in the elevator would also be
`a = (-1.10)\; {\rm m\cdot s^(-2)}\!`.

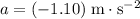Let
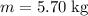`m = 5.70\; {\rm kg}` denote the mass of the box. The net force on the box would be:

`\begin{aligned}(\text{net force}) &= m\, a \\ &= (5.70)\, (-1.10)\; {\rm N} \\ &\approx (-6.27)\; {\rm N} \end{aligned}`.

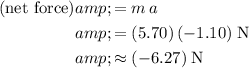The net force on the box is the vector sum of all the forces on it: weight and normal force.

The weight of the box points downward:

`\begin{aligned} (\text{weight}) &= m\, g \\ &= (5.70)\, (-9.81)\; {\rm N} \\ &\approx (-55.917)\; {\rm N}\end{aligned}`.

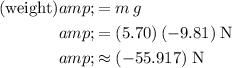The value of the normal force from the ground can be found by knowing the net force on the box:

`(\text{weight}) + (\text{normal force}) = (\text{net force})`.

`\begin{aligned}(\text{normal force}) &= (\text{net force}) - (\text{weight}) \\ &\approx (-6.27\; {\rm N}) - (-55.917\; {\rm N}) \\ &\approx 49.647\; {\rm N}\end{aligned}`.

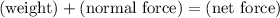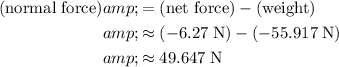In other words, the normal force between the box and the ground would be approximately
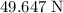`49.647\; {\rm N}` (upward since this value is positive.)

Multiply the normal force on the box by the coefficient of kinetic friction
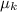`\mu_(k)` to find the value of kinetic friction:

`\begin{aligned}(\text{friction}) &= (\text{normal force})\, \mu_(k) \\ &\approx (49.647\; {\rm N}) \, (0.400) \\ &\approx 19.9\; {\rm N}\end{aligned}`.