Question

How high a hill can a car coast up (engine disengaged) if friction is negligible and its initial speed is 70. 0 km/h

Answer 1

To solve this problem, we can use the principle of conservation of energy. The initial kinetic energy of the car will be converted into potential energy as it coasts up the hill.

The kinetic energy (KE) of the car can be calculated using the formula:

`$$KE = (1)/(2) m v^2$$`

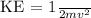
where
`\(m\)` is the mass of the car and
`\(v\)` is its velocity.

The potential energy (PE) of the car at the top of the hill can be calculated using the formula:

`$$PE = m g h$$`

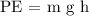
where
`\(g\)` is the acceleration due to gravity and
`\(h\)` is the height of the hill.

Setting these two equations equal to each other (since the initial kinetic energy will be equal to the final potential energy), we get:

`$$(1)/(2) m v^2 = m g h$$`

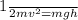
We can solve this equation for \(h\) to find the height of the hill:

`$$h = (v^2)/(2g)$$`

We need to convert the initial speed from km/h to m/s, and we can use the standard value for
`\(g\)` (9.81 m/s²). Let's calculate this.

The car can coast up a hill approximately 19.26 meters high, assuming friction is negligible. This calculation is based on the conservation of energy, where the initial kinetic energy of the car is converted into potential energy as it ascends the hill.