Question

Before radar and sonar, sailors would climb to the top of their ships to watch for land or changes in weather. If the lookout at the top of the mast can see an island seven miles away, about how tall is the mast? Round your answer to the nearest whole number if necessary. Use the formula for the relationship between height (h) and visibility (d)

Answer 1

The formula that relates the distance to the horizon (d) and the height of the observer above sea level (h) is derived from the geometry of the Earth, which is approximately spherical. The formula is:

`$$d = √(2 \cdot h \cdot R)$$`

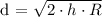
where:

-
`\(d\)` is the distance to the horizon,

-
`\(h\)` is the height of the observer above sea level, and

-
`\(R\)` is the radius of the Earth, which is approximately 3959 miles (or 6371 kilometers).

In this case, we know the distance to the horizon (7 miles) and we want to find the height of the observer (the height of the mast). So we can rearrange the formula to solve for \(h\):

`$$h = (d^2)/(2 \cdot R)$$`

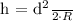
Let's plug in the values and calculate the height.

The height of the mast, rounded to the nearest whole number, is approximately 33 feet.