Question

Given a circle of radius 1 centered at the origin, suppose the point (1,0) on the circle is rotated about the origin by an angle of θ.

a) For what values of θ will the x coordinate of the rotated point be positive? For what values will it be negative?

b) Describe the relationship between the x-coordinate of the rotated point and the values of cos(θ).

c) Compute cos(90°), cos(180°), and cos(270°) using the relationship you described in part b).

pls help they taught me nothing

Answer 1

See below

Explanation:

When
`-(\pi)/(2) < \theta < (\pi)/(2)`, the x-coordinate of the rotated point will be positive since they cover Quadrants I and IV, both of which have positive x-values.

When
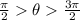`(\pi)/(2) > \theta > (3\pi)/(2)`, the x-coordinate of the rotated point will be negative since they cover Quadrants II and III, both of which have negative x-values.

The x-coordinate of the rotated point will be equal to cosθ since both of these values depend on the angle of θ.

cos(90°) = 0, cos(180°) = -1, and cos(270°) = 0

This is why referring to a unit circle is crucial in understanding this material.