Answer:
1. The integral of
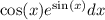 is
is
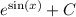 , where
, where
 is the constant of integration.
is the constant of integration.
2. The integral of
 can be rewritten using the double-angle formula as
can be rewritten using the double-angle formula as
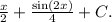
3. The integral of
 is
is
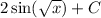 .
.
4. The integral of
![\(\frac{1}{\sqrt[3]{1-7x}} dx\)](https://img.qammunity.org/2024/formulas/mathematics/college/aanqax5n69selva9pipbf4pim6niqxe08w.png) is
is
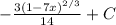 .
.
5. The integral of
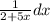 is
is
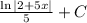 .
.
Explanation:
Let's break down each integral:
1. Integral of
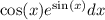
This is a case of a simple substitution. We can let
 , then
, then
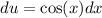 . Substituting these into the integral, we get
. Substituting these into the integral, we get
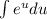 , which is simply
, which is simply
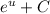 . Substituting back for
. Substituting back for
 , we get
, we get
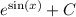 .
.
2. Integral of

The double-angle formula is used here. We know that
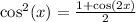 . Substituting this into the integral, we get
. Substituting this into the integral, we get
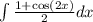 , which can be separated into two simpler integrals:
, which can be separated into two simpler integrals:
 . The integral of
. The integral of
 , and the integral of
, and the integral of
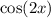 is
is
 . So, the result is
. So, the result is
 .
.
3. Integral of \(\frac{\cos(\sqrt{x})}{\sqrt{x}} dx\)
This is another case of simple substitution. We can let
 , then
, then
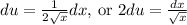 . Substituting these into the integral, we get
. Substituting these into the integral, we get
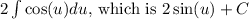 . Substituting back for
. Substituting back for
 , we get
, we get
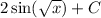 .
.
4. Integral of
![\(\frac{1}{\sqrt[3]{1-7x}} dx\)](https://img.qammunity.org/2024/formulas/mathematics/college/aanqax5n69selva9pipbf4pim6niqxe08w.png)
Here, we can let
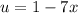 , then
, then
 , or
, or
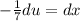 . Substituting these into the integral, we get
. Substituting these into the integral, we get
 , which is
, which is
 . Substituting back for
. Substituting back for
 , we get
, we get
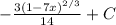 .
.
5. Integral of
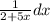
This is a standard form of integral that results in a natural logarithm. The integral of
 is
is
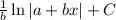 . So, the result is
. So, the result is
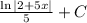 .
.
Hope This Helps!