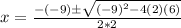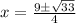Question

Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used. Match each quadratic equation with its solution set. 2x^2 - 8x + 5 = 0 2x^2 - 10x -3 = 0 2x^2 - 8x - 3 = 0 2x^2 - 9x - 1 = 0 2x^2 - 9x + 6 = 0 9+-sqrt33/4 arrowRight _ 4+-sqrt6/2 arrowRight _ 9+-sqrt89/4 arrowRight _ 4+-sqrt22/2 arrowRight _

Answer 1

`\boxed{ (9\pm √(33))/( 4)}\longrightarrow \boxed{2x^2-9x+6=0}`

`\boxed{(4 \pm √(6))/(2) }\longrightarrow\boxed{ 2x^2-8x+5=0}`

`\boxed{ (9 \pm √(89))/( 4) }\longrightarrow \boxed{2x^2-9x-1=0 }`

`\boxed{ (4 \pm √(22))/( 2)}\longrightarrow \boxed{2x^2-8x-3=0}`

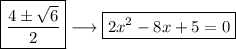
Explanation:

In order to solve for the solution set of a quadratic equation, we can use the quadratic formula:

`\boxed{\bold{x = (-b \pm√(b^2 - 4ac))/(2a)}}`

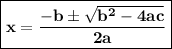
where a, b, and c are the coefficients of the quadratic equation.

For 2x^2-8x+5=0

Comparing the above equation with ax^2+bx+c
In this case, the coefficients are:

a = 2

b = -8

c = 5

Plugging these values into the quadratic formula, we get:

`x = (-(-8) \pm √((-8)^2 - 4(2)(5)))/( 2*2)`

`x = (8 \pm 2√(6))/( 4)`

`x = 2*(4 \pm √(6))/( 4)`

`x = (4 \pm √(6))/(2)`

`\hrulefill`

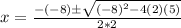
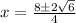
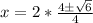
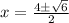
For 2x^2-10x-3=0

Comparing the above equation with ax^2+bx+c
n this case, the coefficients are:

a = 2

b = -10

c = -3

Plugging these values into the quadratic formula, we get:

`x = (-(-10) \pm √((-10)^2 - 4(2)(-3)))/( 2*2)`

`x = (10 \pm √(89))/( 4)`

`\hrulefill`

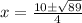
For 2x^2-8x-3=0
Comparing the above equation with ax^2+bx+c
n this case, the coefficients are:

a = 2

b = -8

c = -3

Plugging these values into the quadratic formula, we get:

`x = (-(-8) \pm √((-8)^2 - 4(2)(-3)))/( 2*2)`

`x = (8 \pm 2√(22))/( 4)`

`x = 2*(4 \pm √(22))/( 4)`

`x = (4 \pm √(22))/( 2)`

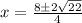
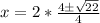
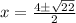
`\hrulefill`For 2x^2-9x-1=0

Comparing the above equation with ax^2+bx+c
n this case, the coefficients are:

a = 2

b=-9

c = -1

Plugging these values into the quadratic formula, we get:

`x = (-(-9) \pm √((-9)^2 - 4(2)(-1)))/( 2*2)`

`x = (9 \pm √(89))/( 4)`

`\hrulefill`

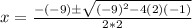
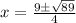
For 2x^2-9x+6=0
n this case, the coefficients are:

a = 2

b = -9

c = -6

Plugging these values into the quadratic formula, we get:

`x = (-(-9) \pm √((-9)^2 - 4(2)(6)))/( 2*2)`

`x = (9\pm √(33))/( 4)`