Question

Locate the Treasury issue in Figure 7.5 maturing in November 2042. Assume a par value of $10,000. a. What is its coupon rate? (Enter your answer as a percent rounded to 3 decimal places, e.g., 32.161.) b. What is its bid price in dollars? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) c. What was the previous day's asked price in dollars? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) Treasury Notes and Bonds

Answer 1

The present value of a bond is determined by discounting future interest payments and the payment of principal using the discount rate. If the discount rate is equal to the coupon rate, such as 8% in the example provided, the bond's present value equals its face value. When interest rates increase, the present value of the bond decreases, which illustrates the inverse relationship between bond prices and interest rates.

Step-by-step explanation:

When evaluating the value of a bond, it is critical to consider the interest or coupon rate, and how changes in the discount rate affect the present value of future payments. We consider a simple two-year bond with a par value of $3,000 and a coupon rate of 8%, which pays $240 in interest annually. To calculate the present value, we need to discount the future cash flows (interest payments and the repayment of principal) back to their present values using the given discount rate.

For the discount rate equal to the coupon rate (8%), the bond's present value is the sum of the present values of the interest payments and the principle. The formula used is PV = (PMT /
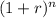`(1 + r)^n`) + (PV /
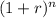`(1 + r)^n`), where PMT represents the payment from the bond (interest), r is the discount rate, and n is the number of periods till the payment. Calculating this for two periods (years) gives us the present value of the bond when the discount rate is 8%.

When recalculating with an increased discount rate of 11%, the present value of the bond will decrease, as the future cash flows are discounted more heavily. This adjustment reflects the inverse relationship between bond prices and interest rates: as rates rise, the value of existing bonds typically falls.

The yield of a bond is the total return anticipated on a bond if the bond is held until the maturity date. It's calculated by taking the annual interest payments plus any capital gains (or losses) and dividing by the initial investment. In the example provided, the bond's yield would be ($1080 - $964)/$964 = 12%, reflecting both the interest payments and the fact that the bond was purchased at a discount due to rising interest rates.