Question

Ninja Co. will pay a dividend of $27.00, which will increase by 3 percent each year over the following three years and then grow at an annual rate of 5 percent forever. You expect a 14 percent return on your invested capital. What price would you pay for a share in this company? (Do not round "PV factor" and other intermediate calculations. Round the final answer to 2 decimal places. Omit $ sign in your response.) Price $

Answer 1

An investor should calculate the present value of expected dividends for the first three years, growing at 3%, and then use the Gordon growth model to find the terminal value, which grows indefinitely at 5%. After discounting these values at a 14% rate of return, the total present value of the expected cash flows is summed to determine the price an investor would pay per share, which would be $328.28.

Step-by-step explanation:

To calculate the price one would pay for a share in Ninja Co., we have to discount the expected dividends back to their present value (PV). First, we need to calculate the annual dividends for the first three years, which grow at a rate of 3%.

1. Year 1 Dividend: $27.00 * (1 + 0.03) = $27.81
2. Year 2 Dividend: $27.81 * (1 + 0.03) = $28.64
3. Year 3 Dividend: $28.64 * (1 + 0.03) = $29.51

Next, we calculate the PV of these dividends using the expected 14% return as the discount rate.

1. PV of Year 1 Dividend: $27.81 / (1 + 0.14) = $24.40
2. PV of Year 2 Dividend: $28.64 /
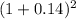   `(1 + 0.14)^2` = $22.03
3. PV of Year 3 Dividend: $29.51 /
   `(1 + 0.14)^3` = $19.87

For the dividends growing at 5% indefinitely from year 4 onwards, we use the Gordon growth model to find the terminal value at the end of year 3 and discount it back to present value.

Terminal Value at end of Year 3 = Dividend at Year 4 / (Required return - Growth rate) = $29.51 * (1 + 0.05) / (0.14 - 0.05) = $35.01 / 0.09 = $389.00

PV of Terminal Value: $389.00 /
`(1 + 0.14)^3`= $261.98

Finally, the total present value of all expected cash flows is the sum of all individual present values: $24.40 + $22.03 + $19.87 + $261.98 = $328.28. Therefore, an investor should pay $328.28 per share for Ninja Co.