Answer:
Approximately
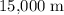 in radius.
in radius.
Step-by-step explanation:
For an object to become a black hole, the escape velocity from its surface should be at least as great as the speed of light in vacuum,
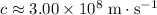 .
.
The formula for escape velocity can be derived the fact that at escape velocity
 , the sum of the kinetic energy of an object
, the sum of the kinetic energy of an object
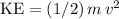 and its gravitational potential energy
and its gravitational potential energy
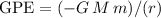 is
is
 :
:
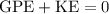 .
.
 ,
,
Where:
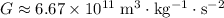 is the gravitational constant,
is the gravitational constant,
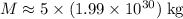 is the mass of this star, and
is the mass of this star, and
 is the radius of this star.
is the radius of this star.
Set escape velocity to the speed of light and solve for radius
 :
:
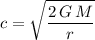 .
.
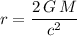 .
.
Substitute in
 ,
,
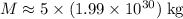 , and
, and
 :
:
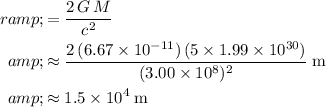 .
.
In other words, the radius of this star should be no greater than
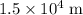 .
.