Question

How many work cycles should be timed to estimate the average cycle time to within 1 percent of the sample mean with a confidence of 99.0 percent if a pilot study yielded these times (in minutes): 4.3, 4.3, 4.8, 4.7, 4.8, and 4.7? (Round the final answer to the nearest whole number.)

Answer 1

Around 3082 work cycles should be timed to estimate the average cycle time to within 1 percent of the sample mean with a confidence of 99%

Explanation:

From the pilot study, we calculate the standard deviation,

Pilot Study Mean = M = (4.3+4.3+4.8+4.7+4.8+4.7)/6

M = 27.6/6

M = 4.6

With this, we calculate the standard deviation,

`S = √(\sum (x - M)^2/N)`

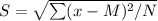
Now, N = 6, and we use N = 6 and not N - 1, because we are only looking at the sample mean and not the whole population,

then, we get S,

S = 0.216

(if you need to form an opinion for the whole population, then S = 0.237)

We need an to be within 1 percent of the sample mean so at most, the margin of error can be 1%

so, margin of error = 0.01,

Now, for a confidence level of 99%, we get and alpha value of,

alpha = 0.01/2 = 0.005

which gives a z value of (-2.57)

z = -2.57,

So, we need to calculate how many work cycles n should be timed,

Using the formula,

`margin \ of \ error = Z(S)/√(n)\\√(n) = Z*(S)/(margin \ of \ error)\\ n = Z^2*(S)^2/(margin \ of \ error)^2\\n = (2.57)^2(0.216)^2/(0.01)^2`

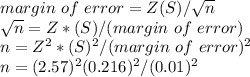
n = 3081.58

n = 3082

So, 3082 work cycles should be timed to estimate the average cycle time to within 1 percent of the sample mean with a confidence of 99%