Question

The human resources office at your college decided to look at how many years 3 employees had worked at the college. The employees had worked at the college for 1, 10, and 6 years. Find the standard deviation of number of years worked for the employees and round to 1 decimal place if needed.

Answer 1

The standard deviation is 3.7 years

Explanation:

To find the standard deviation, we first need to find the mean,

Now, the formula for the mean is,

mean = sum of the terms/number of the terms,

Here, the number of the terms is 3 i.e we have 3 employees,

and the sum will include the sum of the years the 3 employees have worked at the college, so,

Mean = M = (1+10+6)/3

M = 17/3 years

Now, to find the standard deviation,

we use,

since we are only looking at the 3 employees, this is the total population,

and we use the formula for population standard deviation

`\sigma={\sqrt {\frac {\sum(x_(i)-{M})^(2)}{N}}}`

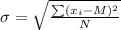
Now, finding the sum,

first we have,

`sum = (1-17/3)^2+(10-17/3)^2+(6-17/3)^2\\= (-14/3)^2+(13/3)^2+(1/3)^2\\=196/9+169/9+1/9\\=366/9\\=122/3`

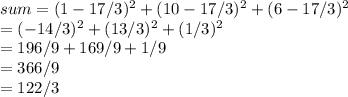
Sum = 122/3,

putting this value into the standard deviation expression,

N = number of employees = 3,

`S = √((122/3)/3) \\S = √(122/9) \\S = √(122) /3\\S = 3.7 years`

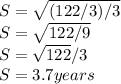
So, rounded to 1 decimal place, the standard deviation is 3.7 years