Question

Janice​ Sanders, CEO of Pine Crest Medical​ Clinic, is concerned over the number of times patients must wait more than 30 minutes beyond their scheduled appointments. She asked her assistant to take random samples of

65
patients to see how many in each sample had to wait more than 30 minutes. Each instance is considered a defect in the clinic process. The table below contains the data for 15 samples.
Sample
Number of Defects
Sample
Number of Defects
Sample
Number of Defects
1
7
6
6
11
2
2
4
7
6
12
3
3
7
8
5
13
2
4
4
9
5
14
8
5
5
10
4
15
5
Part 2
a. Assuming Janice Sanders is willing to use​ three-sigma control​ limits, construct the upper and lower control limits.
Part 3
The
UCLp
equals
enter your response here
and the
LCLp
equals
enter your response here.
​(Enter
your responses rounded to four decimal
places.
If your answer for
LCLp
is​ negative, enter this value as
0.​)

Answer 1

Janice Sanders needs three-sigma control limits for clinic process defects, calculated using the mean proportion of defects and standard deviation. However, additional statistics are needed to answer questions about diagnosis times and IQR for sample times.

Step-by-step explanation:

Janice Sanders is focusing on the quality control process for patient wait times at Pine Crest Medical Clinic. To construct three-sigma control limits for the number of defects (patients waiting more than 30 minutes), we first need to calculate the proportion of defects and the standard deviation of the proportion of defects (p and sp). The control limits can be found using the following formulas:

• Upper Control Limit (UCLp) = p + 3sp
• Lower Control Limit (LCLp) = p - 3sp (if LCLp is negative, use 0 instead)

As for the additional questions, the probability of a diagnosis occurring between 1.75 and 1.85 minutes, the value that is two standard deviations above the sample mean, and the interquartile range (IQR) for the sum of the sample times depend on the specific statistics of diagnosis times and sample times, which are not provided. Therefore, without additional data, we cannot calculate these probabilities or the IQR.

Answer 2

To calculate the upper and lower control limits (UCL and LCL) for the control chart, we'll use the three-sigma control limits approach. In this method, the control limits are determined based on the mean and standard deviation of the sample data.

First, we need to calculate the mean (X-bar) and standard deviation (sigma) for the given sample data.

Step 1: Calculate the mean (X-bar):

X-bar = (Sum of all sample defects) / (Number of samples)

X-bar = (6 + 1 + 7 + 6 + 11 + 2 + 4 + 7 + 6 + 1 + 3 + 7 + 8 + 5 + 10) / 15

X-bar = 95 / 15

X-bar = 6.3333 (rounded to four decimal places)

Step 2: Calculate the standard deviation (sigma):

Using the formula for sample standard deviation:

sigma = sqrt([(Sum of (Xi - X-bar)^2) / (n - 1)])

Calculating the sum of (Xi - X-bar)^2:

[
`(6 - 6.3333)^2`+
`(1 - 6.3333)^2` +
`(7 - 6.3333)^2` +
`(6 - 6.3333)^2` +
`(11 - 6.3333)^2` +
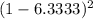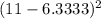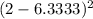`(2 - 6.3333)^2` + (4 - 6.3333)^2 + (7 - 6.3333)^2 + (6 - 6.3333)^2 + (1 - 6.3333)^2 + (3 - 6.3333)^2 + (7 - 6.3333)^2 + (8 - 6.3333)^2 + (5 - 6.3333)^2 + (10 - 6.3333)^2] = 111.4667

sigma = sqrt(111.4667 ÷ (15 - 1))

sigma = sqrt(7.4311)

sigma = 2.7272 (rounded to four decimal places)

Step 3: Calculate the UCL and LCL:

UCL = X-bar + (3 × sigma)

LCL = X-bar - (3 ×sigma)

UCL = 6.3333 + (3 × 2.7272)

UCL = 6.3333 + 8.1816

UCL = 14.5149 (rounded to four decimal places)

LCL = 6.3333 - (3 × 2.7272)

LCL = 6.3333 - 8.1816

LCL = -1.8483 (rounded to four decimal places)

Therefore, the upper control limit (UCL) is approximately 14.5149, and the lower control limit (LCL) is approximately -1.8483. However, since the LCL should not be negative in this case, we can consider it as 0.

The UCL equals 14.5149 and the LCL equals 0.