Question

What is the effective interest rate of a simple discount note for $26,900, at an ordinary bank discount rate of 15%, for 30 days? Assume that there are 360 days in a year. The effective interest rate is %. (Round to the nearest tenth as needed.)

Answer 1

The formula for calculating the effective interest rate on a simple discount note is:

`{\text{Effective Interest Rate} = \frac{\text{Discount}}{\text{Face Value}} * \frac{360}{\text{Days}}}`

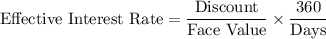
where:

• Discount is the interest charged on the loan.
• Face Value is the amount borrowed.
• Days is the length of the loan in days.

In this case, the Face Value is $26,900, the Ordinary Bank Discount Rate is 15%, and the Days is 30. We need to calculate the Discount first:

`\text{Discount} = \text{Face Value} * \text{Ordinary Bank Discount Rate} * \frac{\text{Days}}{360}`

`\text{Discount} = \$26,900 * 0.15 * (30)/(360)`

`\text{Discount} = \$403.50`

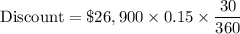
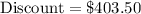
Now we can plug in the values into the formula for Effective Interest Rate:

`{\text{Effective Interest Rate} = \frac{\text{Discount}}{\text{Face Value}} * \frac{360}{\text{Days}}}`

`{\text{Effective Interest Rate} = (\$403.50)/(\$26,900) * (360)/(30)}`

`{\text{Effective Interest Rate} = 0.015 * 12}`

`{\text{Effective Interest Rate} = 0.18 \text{ or } 18\%}`

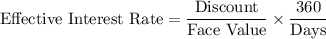
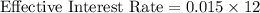
`\therefore` The effective interest rate on the simple discount note is 18%.

`\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}`