The average speed formula is given by:
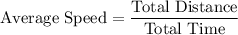
Let's calculate the total distance first. The car travels 120 miles from point A to point B, and then returns the same distance. Therefore, the total distance is
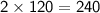 miles.
miles.
Now, let's calculate the total time. The time taken to travel from A to B can be calculated using the formula
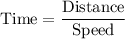 .
.
For the journey from A to B:
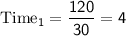 hours
hours
For the return journey from B to A:
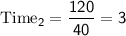 hours
hours
The total time for the round trip is the sum of the individual times:
 hours
hours
Now, we can calculate the average speed:
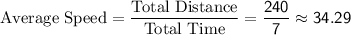 miles per hour.
miles per hour.
Therefore, the average speed for the round trip is closest to 34.29 miles per hour.