Answer:
The vertex of the function is at (–3,–16)
The graph is increasing on the interval x > –3
The graph is positive only on the intervals where x < –7 and where
x > 1.
Explanation:
The graph of
 has clear zeroes at
has clear zeroes at
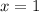 and
and
 , showing that
, showing that
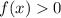 when
when
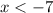 and
and
 . To determine where the vertex is, we can complete the square:
. To determine where the vertex is, we can complete the square:
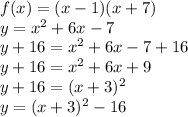
So, we can see the vertex is (-3,-16), meaning that where
 , the function will be increasing on that interval
, the function will be increasing on that interval